Computational Systems for Sound Fields, as Tools in Design and Diagnosis


January 2000

Masatsugu Sakurai

Graduate School of Science and Technology
Kobe University

Preface

 This dissertation is submitted for the Doctor of Philosophy Degree to The Graduate School of Science and Technology, Kobe University, Japan.
The theme of this study is using computational systems as tools in design and diagnosis. The main feature of this computational system is that the whole system is based on a subjective preference theory that is itself based on a model of the auditory-brain system. Such a system could be expected to lead to many important acoustic discoveries, because its design and diagnostic function include the objective and the result of the study of subjective preference based on the auditory-brain system model. Through the course of these studies, such discoveries were made and incorporated into the system, making them into its own features and characteristics.

Acknowledgments

I would like to express my thanks to Professor Yoichi Ando, Kobe University, and the members of Ando Laboratory, especially, Mr. Hiroyuki Sakai, Dr. Shin-ichi Sato, and Mr. Yukio Suzumura, and Mr. Shinichi Aizawa, Yoshimasa Electronic Inc., who has helped me in many respects concerning the system development for this study.

Chapter 1 Introduction

1.1. Previous Studies Relating to Computational Systems for Sound Fields

Introduction
 To realize an excellent sound field in a concert hall, it is important to identify the orthogonal factors influencing subjective evaluation. Using dissimilarity tests, Yamaguchi found two significant physical factors, the sound pressure level and the reverberation characteristics [1]. Edward also tested dissimilarity, and reported the early-echo pattern, the reverberation time RT, and the volume level to be the significant factors [2]. Schroeder, Gottlob, and Siebrasse [3] avoided using ill-defined adjectives, such as "intimate", "warm", "rich", and "clear", by conducting subjective preference tests. They found two significant factors, RT and the interaural crosscorrelation (IACC), defined by Damaske and Ando [4]. Kimura and Sekiguchi found reverberance and loudness to be significant factors [5]. Wilkens found that perception of strength and extension of sound source, perception of clarity, and tone color are significant subjective attributes [6]. Systematic investigations by Ando were made to find the orthogonal factors in subjective preference for sound Gelds [7]. Ando described four orthogonal physical factors (the listening level LL, the initial time delay gap Dt1, the subsequent reverberation time Tsub, and the IACC), which determine the scale values of subjective preference for simulated sound Gelds. From subjective questionnaires, Barron found that the reverberation time, the early decay time, the early-to-late sound index C80, the total sound level, and the early lateral energy fraction were significant subjective factors [8, 9]. Beranek suggested adding two more factors to Ando's four physical factors, the Bass ratio (BR) and the Surface Diffusivity Index (SDI) [10]. Problems with regard to both objective and subjective orthogonalities in above two investigations still remain. As far as subjective preference is concerned, it is worth noting that the sound fields in a real concert hall for listeners facing to the performers (IACC is obtained at t = 0) can be described by only four orthogonal physical factors [11, 12].

The theory of subjective preference
    Four orthogonal physical factors have been identified from the systematic investigation of sound fields simulated by computer and listening tests (paired-comparison tests) [7]. Several reverberation free music signals were used to simulate sound fields from which fully independent physical parameters of the sound signals could be determined. The law of comparative judgments enables us to construct a linear scale value of subjective preference. The optimum design objectives can be described in terms of subjectively preferred sound qualities, which are related to comprehensive criteria consisting of temporal and spatial parameters describing the sound signals at the two ears.

(1)Listening level
    The listening level is, of course, the primary criterion for listening to the sound field in concert halls. The absolute preferred listening level depends upon the musical program and the particular passage being performed. The listening level LL is given by

LL = 10 log ( 1 + A2 ) - 20 log d0 - 11 [dB],

(1)
where A is the total pressure amplitude of the early reflections and subsequent reverberation, and d0 (= | r - r0|) is the distance between the source and the listener's position.

(2)Initial time delay gap
    The relationship between the autocorrelation function (ACF) of the source signals, the total pressure amplitude of the early reflections and subsequent reverberation, and the most preferred delay time of a single reflection has been obtained from the approximate formula [7, 13]

[Dt1]p (1 - log 10 A) 

(2)
where the total amplitude of the reflections A is given by

(3)
Ai (i = 1, 2, ..., N) being the pressure amplitude Of each reflection relative to that of the direct sound, N is selected a large number for the convergence. The quantity te is the effective duration of the ACF with a 10-percentile delay, defined as the delay at which the envelope of the normalized autocorrelation function becomes 0.1.

(3)Subsequent reverberation time
    For flat frequency characteristics of reverberation, the preferred subsequent reverberation time after early reflections is described simply in terms of the effective duration of ACF of the source signals [14, 15], as given by

[Tsub]p 23te

(4)

(4)IACC
    The IACC and subjective preference show a negative correlation for all available data. That is, listeners prefer dissimilar signals for the left and right ears. This holds only under the condition that the maximum value of the interaural crosscorrelation function at an interaural time delay equal to zero is maintained to ensure frontal localization of the source [12]. Otherwise, an image shift of the source or an unbalanced sound field may be perceived, and the value of preference decreases.

(5)A-value
    The A-value is not included in the orthogonal physical factors, however, it is a factor used for calculating the most preferred delay time of a single reflection related to the autocorrelation function (ACF) of the source signals (equation 2). The A-value also is related to calculating the listening level by equation (1). It is worth noting that the "Hallradius"[16] defined by the distance between the source position and the positions in which the pressure amplitude of the early reflections and subsequent reverberation is equal to the total pressure amplitude of the direct sound (A = 1).
    Independent effects of the four objective factors were examined by several experiments as shown in Table 1.1 [14, 17, 18, 19, 20]. The theory of subjective preference for each seat in a concert hall is described based on these results. The linear scale value of preference has been obtained using the law of comparative judgments [21] and reconfirmed by the goodness of fit [22]. Furthermore, the units derived from experiments with different sound sources and different subjects were almost equal [7], so the scale values may be added to give

S s1 + s2 + s3 + s4

(5)
where si (i = 1,2,3,4) is the scale value obtained in relation to each objective parameter. Equation (5) indicates four-dimensional continuity. Since the scale value is relative, it may conveniently be set equal to zero for the preferred conditions, without any loss of generality.
According to the behavior of the scale value in relation to each objective parameter, the resulting expression for si is given by

si -ai | xi |3/2

(6)
where the parameter xi and the coefficients ai for global subjects are listed in Table 1.2. Here, P is the sound pressure at the seat, and [P]p is the most preferred sound pressure that may be assumed at a particular seat position in the room under investigation.
    Cocchi, Farina, and Rocco were the first to report that the subjective preference for sound Belds in an existing hall calculated using the four orthogonal physical factors for different source signals agreed with subjective judgments [11]. Sato, Mori, and Ando found that the scale values of subjective preference obtained in changes of source location for a number of listeners at fixed seats in an existing hall agreed with the calculated scale values, when a further parameter, interaural time delay tIACC was added to the four orthogonal physical factors [12]. The interaural time delay tIACC relates to the horizontal sound localization and responds to the image shift due to strong reflections or an unbalanced sound field.
    Recently, the theory of subjective preference using the four orthogonal physical factors was applied to the acoustic design of the Kirishima International Concert Hall in Kyushu [23]. During the design process, the four orthogonal physical factors at each seat in the concert hall were calculated for several different designs of the hall. After construction of the concert hall, acoustic measurements were performed. To enhance individual satisfaction, the seat selection system testing individual subjective preference of sound fields was introduced.

Table 1.1. Examinations on independent effects of each two of four objective factors on the subjective preference judgements. *Effects of Dt1 ware examined under conditions of greatly different fixed SL.
Factors LL Dt1 Tsub IACC
LL --- Ando & Okada None Ando & Morioka [17]
Dt1(SD) --- Ando, Okura & Yuasa [14] Ando & Imamura [18];
Ando & Gottlob
Tsub --- Ando, Otera & Hamana [20]


Table 1.2. Objective parameters and coefficients (global subjects).
i xi ai
xi >= 0 xi < 0
1 0.07 0.04
2 1.42 1.11
3 0.45 + 0.74A 2.36 - 0.42
4 Interaural crosscorrelation (IACC) 1.45 -


Physiological responses to sound fields
    It is quite natural to assume that subjective preference is reflected by brain activity or physiological responses.
    The relationship between the slow vertex response (SVR) and subjective preference has been investigated systematically [24]. The SVR was recorded by averaging the evoked potentials responding to auditory stimuli, such as clicks, noise and speech. An adjustable test stimulus was presented alternately with a reference stimulus. The pair of stimuli was presented 50 times to integrate and average the evoked potentials, and the SVRs were obtained from the left and right temporal area (T3, T4: according to the International 10-20 system [25]). The results show that the latency of N2-components, that is, the interval between the time the stimulus was presented and the time of the second negative peak of the SVR, corresponded significantly to the subjective preference for changes of the sensation level SL, the delay time of single reflection Dt1, and the IACC, respectively [24, 26, 27]. The longest latencies are always observed for the most preferred condition, revealing that most of the brain is relaxed under the preferred condition. Furthermore, it is remarkable that hemispheric dominance appeared in the amplitude of the early stage of the SVR. In the results the amplitude of A(P1 - N1), Which is the amplitude of the first positive peak to the first negative peak, shows that the hemispheric dominance differed as acoustic factors changed. The left hemisphere was dominant when the Dt1 was varied and the right hemisphere was dominant when SL or IACC were varied.
    The evoked-potential methods cannot be applied to changes of the reverberation time with signals longer than 0.9s, therefore a method for analyzing a continuous brain wave was developed. When a pair of stimuli are presented, the continuous brain wave can be recorded. The effective duration of ACF, te, of the a-waves for the continuous brain wave was analyzed for changes in the delay time of the single reflection and the reverberation time, respectively. It is noteworthy that the te of a-waves are longer only in the left hemisphere for the preferred conditions [Dt1]p and [Tsub]p [28, 29]. This may be interpreted as being caused by a similar repetitive feature in the a-waves evoking comfortable relaxation repeatedly in the mind.
    Thus, the subjective preference can be traced back to a imitive response seen as gross brain activity that corresponds well with the scale value of subjective preference. Also, the evidence indicates that the left hemisphere dominance of the temporal factors (Dt1 , Tsub) and the right hemisphere dominance of the spatial factors (IACC and SL) may independently influence subjective preference values [30].


Design process using the temporal and spatial factors

Design procedure
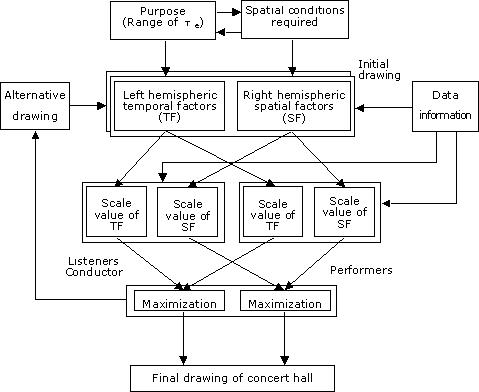
    The fundamental concept for the acoustic design of a concert hall was derived from the above theory and is illustrated in Figure 1.1. The specialization of the left and right hemispheres for temporal and spatial factors should be taken into consideration for both listeners and performers. Alternative drawings, for increasing the scale values of preference, should be determined using the data information. The first step is to determine the dominant use of the concert hall under design by selecting a certain range of the te for the source programs, which depends on the type of music and its tempo. The second step is to form the initial drawings of the enclosure so as to optimize the spatial factor IACC. The final goal is to maximize the scale values of preference for both the listeners and the performers, and this is reflected in the final drawing of the concert hall.

Figure 1.1. Flow chart for the design of concert hall



1.2. Purpose of This Thesis
The science technology calculation system which is the basis of measurement and psychological evaluation of the environmental noise, including sound fields in a room, is indispensable to this fields' study, so its realization have been hoped. Our study tried to make the computational systems for sound fields, as tools in design and diagnosis based on the model of auditory-brain system, and used it for the concert hall actually.

| NEXT |