Home  

| Japanese | English |

Introduction to the autocorrelation function (ACF)

In the sound measurement and analysis software, DSSF3, sound is analyzed by use of the ACF in addition to the conventional FFT analysis.  We provide some information about the ACF in this page.

1. Introduction

Sound is a variation of the air pressure transmitted from a sound source. The pressure variation can be expressed as a waveform. Sound is transmitted with progress of time. If time does not exist, we cannot hear sound. Please keep in mind that the ACF is a useful tool by which we can investigate sound in the time domain.


2. Time domain and frequency domain of sound

There are two methods of describing sound. One is the method in the time domain ("waveform" or "ACF", as functions of time). The other is the method in the frequency domain ("spectrum" as a function of frequency). These two methods describe a same sound from different points of view, and the conversion from each other is possible. That is, although sound can be similarly described effectively whichever we use, one of methods is more convenient than another in some situation. For example, you often see the bar graph (graphic equalizer) in a component stereo. It shows the frequency distribution of sound. You can grasp easily that how much amount of low-pitched sound or high-pitched sound is contained. In contrast, the ACF analysis that we offer is effective in order to focus on the temporal information of sound such as periodicity or sudden transition.


3. The relation between sound and our brain

The sound coming into the ear progresses along a hearing pathway, and is perceived with the passage of time. At this time, the meaning of the sound is interpreted by our brain at every moment. Here is the importance of analyzing sound in time domain. Except that the ACF describes the sound in time domain, the same mathematical information is expressed in the power spectrum. However, the ACF analysis differs from the spectrum analysis greatly in that the higher-level processes in our auditory brain are taken into consideration. If you are interested in the neural mechanism of analyzing sound by use of the ACF, visit cariani.com to see the latest research topics. 


4. What is autocorrelation function?

Autocorrelation function (ACF) is defined by the following formula.

- - - - - -(1)

Here, p(t) is the sound waveform, t is the delay time and 2T is the integration interval. As explained previously, the analyses in the time domain and the frequency domain are mutually convertible. When the power spectrum of a sound signal is defined as Pd (w), the ACF (F(t)) is obtained as follows.

- - - - - -(2)

- - - - - -(3)

Thus, ACF and the power spectrum include the same information mathematically. Now, let us consider the physical meaning of the ACF.


Fig.1 The physical meaning of the autocorrelation function and the sound signal at t= 0 and t=t1 

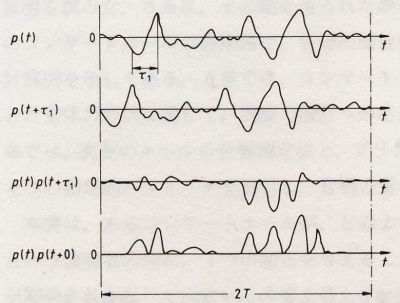
As shown in Fig. 1, let's consider the signal p(t) and its delayed version p(t+t). If the amplitude of p (t) and p (t+t) is large, and two signals are similar, the correlation value of two signals, Fp(t) becomes large. So, it can be said that the ACF is the function that shows how much similarity is included in the signal itself. The ACF is a useful tool in the signal analysis because it can be used to detect the periodicity of the signal. Below, the examples of the ACF for music and noise are shown.

Music


Time [ms]
Noise


Time [ms]

We can see that the ACF of the noise signal becomes small immediately. This means that the similarities between the original signal and the time delayed signal are low, because various sound components are contained in noise. In contrast, the ACF of the music has several periodicities and decreases gradually. The maximum peak found at 20 ms corresponds to the fundamental frequency of the signal. We can see that the ACF is repeated with this fundamental period (peaks are found at 40 ms, 60 ms, and 80 ms). In most cases, the fundamental frequency is perceived as pitch. Other peaks within the fundamental period corresponds to the strong harmonics. 


5. Significant parameters from the ACF

Any sound signals (e.g. music, environmental noise, speech, singing voice) can be analyzed using the following four factors extracted from the ACF.

(1) Average sound energy: F(0)
It expresses the power of sound. There is a close relationship between F(0) and the subjective scale of loudness.

(2) Effective duration of the ACF: te
This is defined as the delay time where the envelope of the normalized ACF decays to 0.1. The reverberation component contained in the signal itself is expressed. For example, slow orchestra music has much longer te than speech. Here, the normalized ACF is defined by the following formula.

- - - - - -(4)

The figure below shows the definition of te. The ACF plotted in the logarithmic scale can be fitted by the linear regression in most cases. 

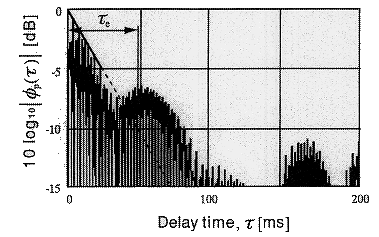
(3) Time delay of the maximum peak: t1
This corresponds to the pitch of sound.

(4) Amplitude of the maximum peak: f1
This corresponds to the pitch strength of sound.

6. Application of the ACF

As shown above, the factors extracted from the ACF have close relation with the subjective attributes of sound. In the field of architectural acoustics, the most preferred delay time of the reflective sound and the reverberation time can be calculated by using the effective duration of the music signal's ACF. By this approach, design of the excellent concert hall has been attained. Basic research using the ACF analysis can be found at http://www.andolab.org/
Home