| Japanese | English |

Strike a knee with a tuning fork. And place the fork to the body of a guitar to make it resonant with it. A beat is heard if the pitch of the sound of a tuning fork and a guitar is not same. Tension of the string is adjusted so that the beat disappears and these become one sound. However, the tuning fork does not sound for a long time. I had to strike my knee repeatedly until I was getting used to the tuning.
Now, let's use the "signal generator" instead of a tuning fork.
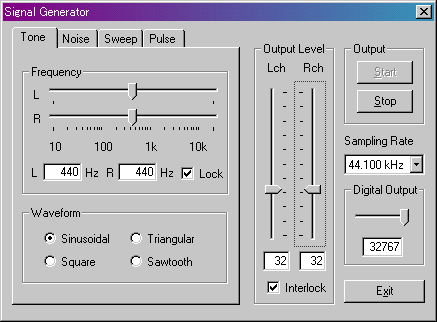
A 440Hz sinusoidal tone comes from the built-in speaker of PC. Tune the fifth string to match this note. Unlike a tuning fork, it is continuously sounding. You need not to be hurried.
The simplest tool for seeing sound is the oscilloscope. I think that the difference in frequency can be seen easily, because the real time waveform is displayed on the screen. To measure sounds from the guitar and the speaker (sine tone), a microphone was connected to PC's microphone port. Then, I picked the fifth string while generating 440Hz sine tone by the signal generator.
However, by using the PC's built-in speaker, the waveform could not be seen as sine wave (because of the poor quality). Also, since the one point stereo microphone was used, PC's sound and a guitar sound could not be separated. As a result, the measured sound was displayed as shown in the following figure. Two sounds are mixed and I can't even find the frequency of the note.
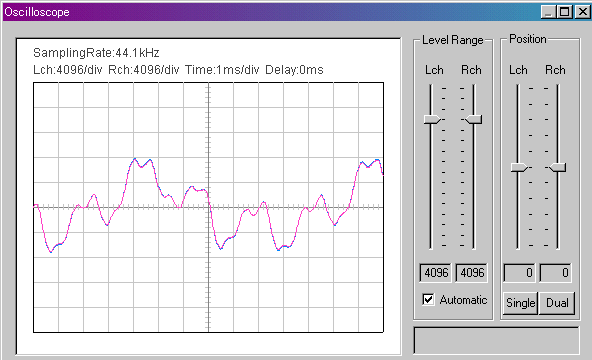
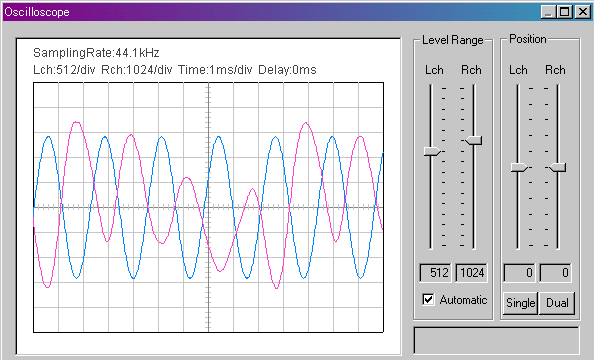
To separate two sounds, I tried to feed two signals into the independent channels. As an input device, I use USB audio interface, Edirol UA-5 *. The signal generator's output was fed to the left channel, and the guitar sound captured by the microphone was fed to the right channel via Sony's microphone mixer.
* In the picture, Edirol UA-3, instead of UA-5, is used. But we don't recommend UA-3, because we have heard many problems in using this device.

A blue curve is the signal generator's output and a red curve is the guitar sound. Now, the sounds can be seen separately. But there is another problem... The blue waveform (signal generator) is a clean sine wave, but the red waveform (guitar) is fluctuating very much, because the guitar sound decays rapidly. Also, the guitar sound is not a simple sine wave. I think it is difficult to tune with the oscilloscope.
Next, let's see the power spectrum. The "frequency range" is set to 100-1,000Hz.
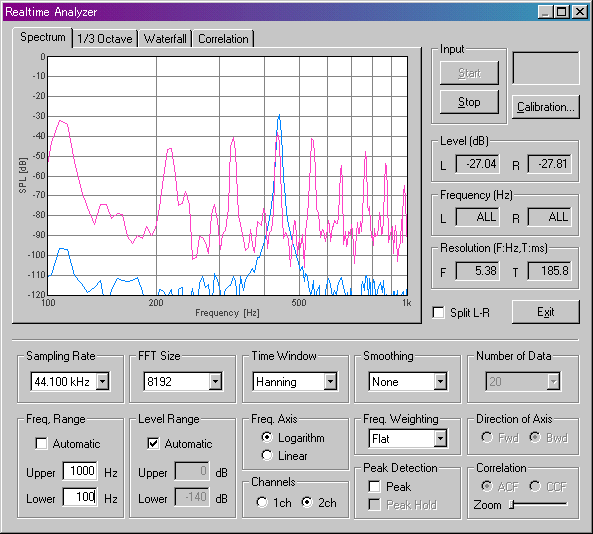
A peak at 440 Hz is clearly seen for a blue graph (sine wave). In red graph, many peaks can be seen, roughly at 110, 220, 330, 440, 550, 660, 770, 880, 990 Hz. These peaks are the frequency components called harmonics. It is difficult to read the slight difference to the reference note.
Then, how about seeing with the correlation function? Open the real-time analyzer's "correlation function" tab, and set the correlation function as CCF (Cross-Correlation Function) at the lower right of a window.
The cross-correlation function is "a function to show the degree of similarity of two signals." Graph is 0 only by the sine wave of Left channel.
When the guitar sound is put in from the right channel, the display changed as shown below. CCF is a sine wave of 440 Hz (see that its period is 1000/440=2.27 ms). This means that two sounds are almost matched in frequency.
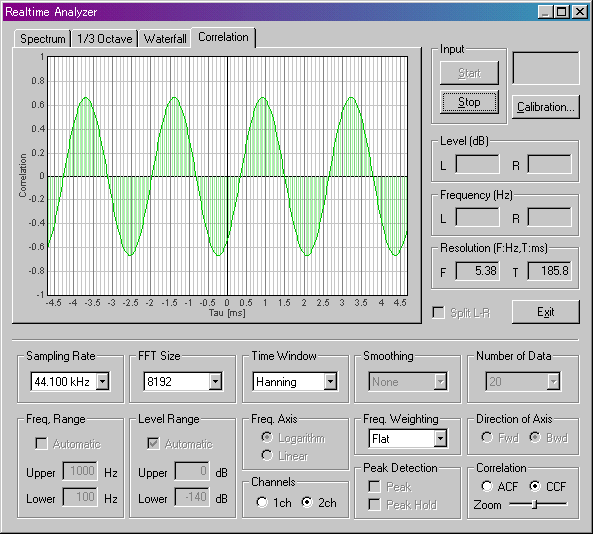
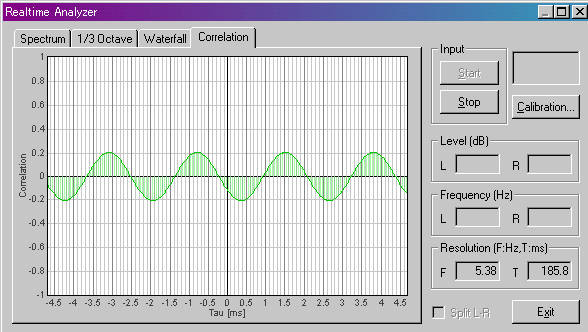
If the tuning is slightly mismatched, the CCF waveform will scroll from right to left (or from left to right). If the tuning is done well, the waveform will stop.
It turned out that the tuning of the acoustic guitar can be performed using the cross-correlation function. But it was found that the cross correlation reacts not only to the fifth string (A) but to the fourth string (D). The result is shown below. Same as above, the 440Hz sine wave is fed into the left channel, and the guitar sound to the right channel.
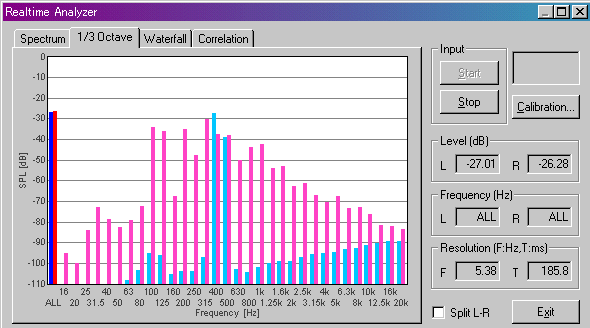
This is the 1/3 octave analysis of the fifth string open (A). Blue bar is the
440Hz sine wave and the red bar is the guitar sound. Many harmonics are visible.
This is the power spectrum of the open fifth string (A).
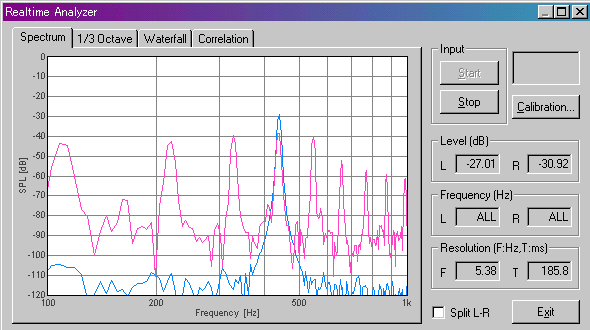
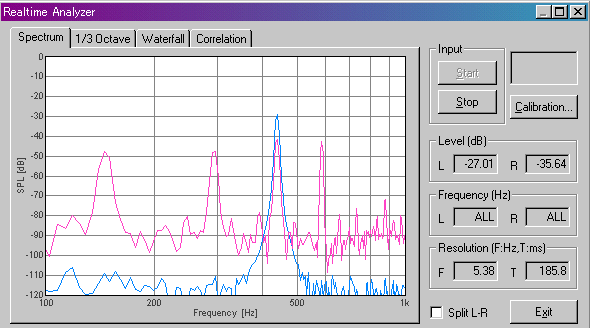
This is the power spectrum of the open fourth string (D). 440Hz is
included in this note too. Probably this is the reason why the CCF reacted to
this note.
In the following, frequencies of the equal temperament scale are shown. Since one octave consists of twelve semi notes, frequencies of each scale become A*2^ (n/12).
| Musical scale | Frequency (Hz) |
| A | 440.0 |
| A# | 466.1 |
| B | 493.8 |
| C | 523.2 |
| C# | 554.3 |
| D | 587.3 |
| D# | 622.2 |
| E | 659.2 |
| F | 698.4 |
| F# | 739.9 |
| G | 783.9 |
| G# | 830.6 |
| A | 880.0 |
According to the table, the frequency of D is 587.3Hz. Actually, this frequency is seen in the power spectrum. But why 440 Hz is included in this note? This is not a harmonics of D...
Two notes with a pitch ratio of 1:2 has the relation of one octave. Two notes of 2:3 and 3:4 are called fifth and fourth chord. When the frequencies of two sounds have integer ratios like this, those sounds are heard in harmony as a chord. It turns out that 440Hz (A) is equivalent to the fourth chord of 587Hz (D). Similarly, the spectrum of the fifth string has a peak at 330 Hz (fourth of 440 Hz).
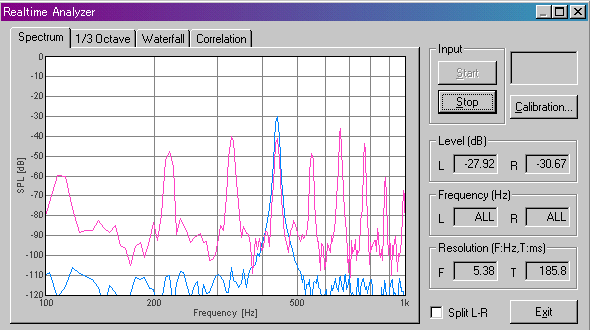
To see whether this is peculiar to a guitar sound, let's see the power spectrum of A and D of a piano sound.
This is the spectrum of the A of a piano sound.
This is the spectrum of the piano sound D.
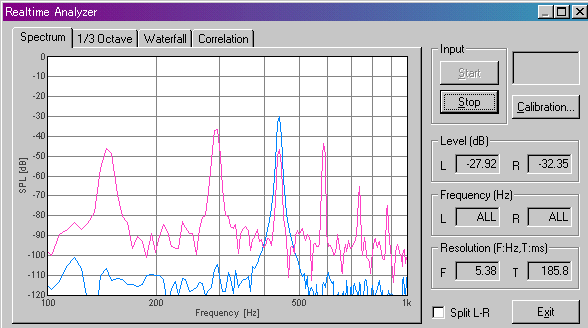
Spectrum looks like a guitar sound although strength of each component is different. It seems that 440Hz is contained also in D of piano.
As seen so far, tuning of the musical instrument is possible by using the realtime analyzer. First, generate the tone of the fundamental frequency (it was A in this case) by the "signal generator". Tune roughly the sound of a musical instrument with this sound. Finally, tune finely by the "cross-correlation" function.
November 2002