| Japanese | English |

This device is compact as a business card and operates by two dry cells.

In the photo above, the guitar is tuned with the open fifth string. It is displayed on the upper right of a screen as A, and the needle inclines to right a little. It means that the sound is slightly higher than A. What is necessary is just to tune up so that a needle comes to a center.
I have bought a new string (Martin Light) too. I replaced strings and tried tuning by the automatic tuner. Bu I found a big problem with this tuner. When I tuned to A4, one-octave-lower A (A3) was also tuned. If those who know nothing about guitar used this tuner, all strings might be tuned as lower octaves. (Actually, it is OK because the tuner has a function to sound the fundamental tone too.)
Now, after the fifth string is tuned to A4 (440Hz), other strings will be tuned on the basis of it. When I picked the open sixth string after a rough tuning, it was displayed as E. Also, it was displayed as D for the open fourth string. All strings can be tuned like this.
However, the open sixth string is E and the open first string is also E. It seems that those are the same note for the tuner even if two sounds are 2 octave apart. The measurement range of this tuner is said as "C1 (32.70Hz) - a C8 (4186. 01Hz): sin wave." It may be the mechanism that displays the scale corresponding to the harmonic structure of 12 temperament within the range. However, as investigated last time, a single sound of a guitar contains fourth and fifth chords in addition to its harmonics. How does the tuner discriminate the fundamental frequency among many harmonics?
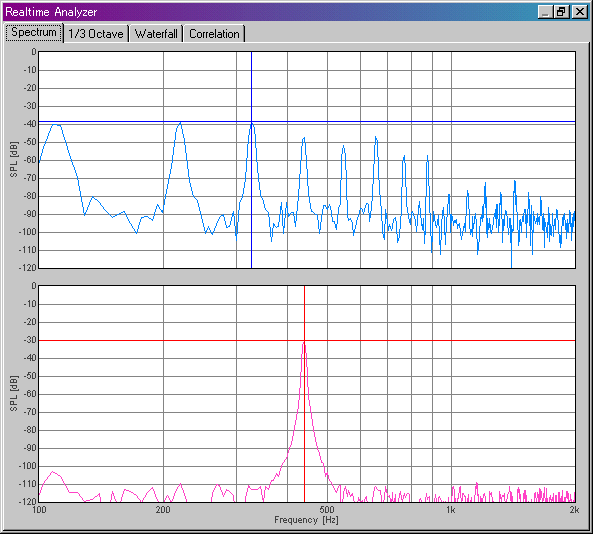
The power spectra of two channels are displayed. The software used is Realtime Analyzer of DSSF3. The frequency range is 100-2,000Hz. Lower screen is of 440Hz sine tone (output of the signal generator) and the upper screen is of the open fifth string of a guitar. The red and blue cross lines indicate the peak frequencies. As we can see, the fundamental frequency is not necessarily the strongest component. Peak values actually move back and fourth during the measurement.
I tried an experiment in which a scale is judged by the tuner for a test signal. The test signal was generated by the "signal generator".
When the sin waves of D4 (588Hz) and A4 (440Hz) were generated simultaneously, the tuner
recognized this sound as D.
When 588Hz (D4) and 880Hz (A5) were generated, the tuner's display changed between A and D repeatedly. It seems the tuner is very confused. In the case of 588Hz (D4) and 784Hz (G5), the tuner judged as D. It does not seem that the frequency of the higher tone is always chosen.
The power spectra for every scale within one octave were investigated using the electronic piano (YAMAHA). I used piano because I can make sound by one hand unlike guitar. What is necessary is to type a keyboard with the right hand and to click the Alt+PrintScreen key with the left hand to capture a screen copy of the measurement screen.
Below is the results. Fundamental frequency is noted following a scale name. See the graphs below B while paying attention to the 220Hz peak of the graph of A. It turns out that the peak moves to the right little by little.
A-110, 220, 440, 880, 1760, 3520Hz
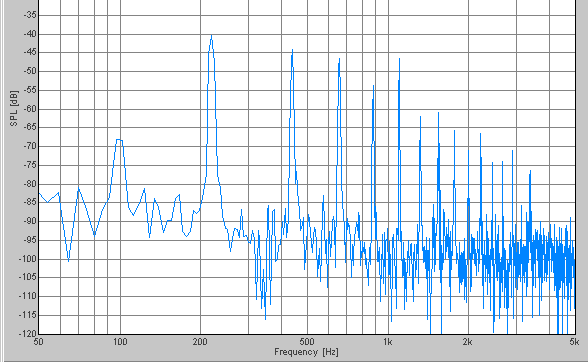
B-123.45, 246.9, 493.8, 987.6, 1975.2, 3950.4Hz
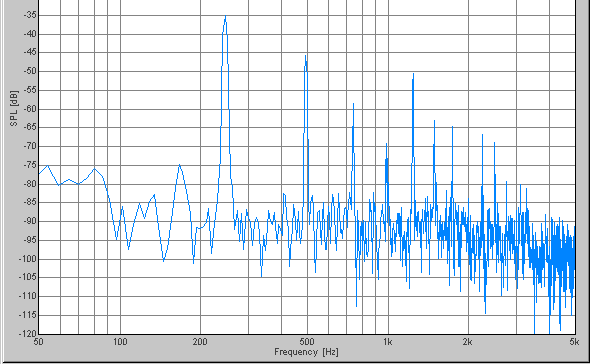
C-130.8, 261.6, 523.2, 1046.4, 2092.8, 4185.6Hz
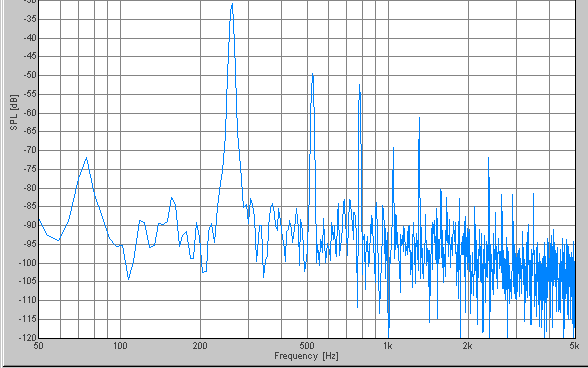
D-146.825, 293.65, 587.3, 1174.6, 2349.2, 4698.4Hz
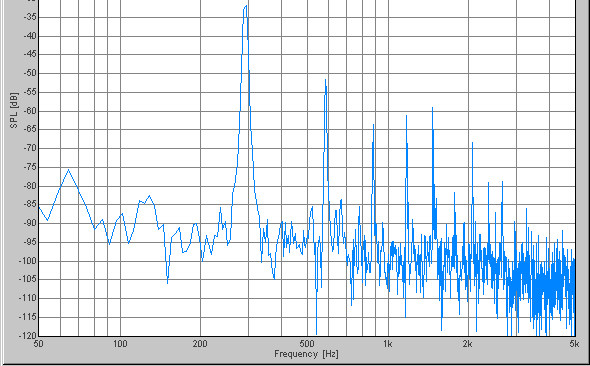
E-164.8, 329.6, 659.2, 1318.4, 2636.8Hz
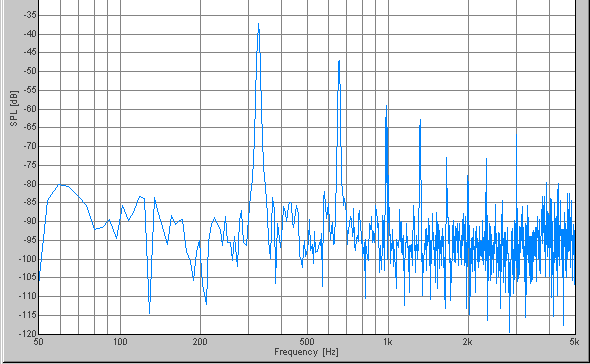
F-174.6, 349.2, 698.4, 1396.8, 2793.6Hz
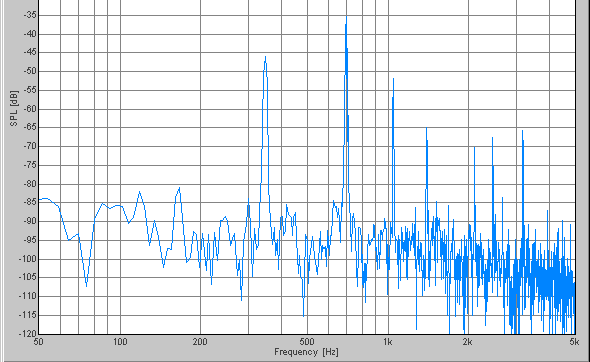
G-195.975, 391.95, 783.9, 1567.8, 3135.6Hz
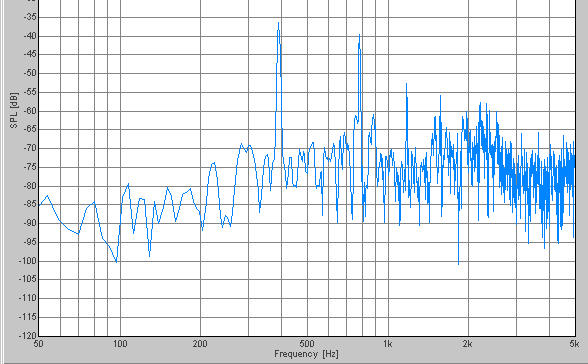
A
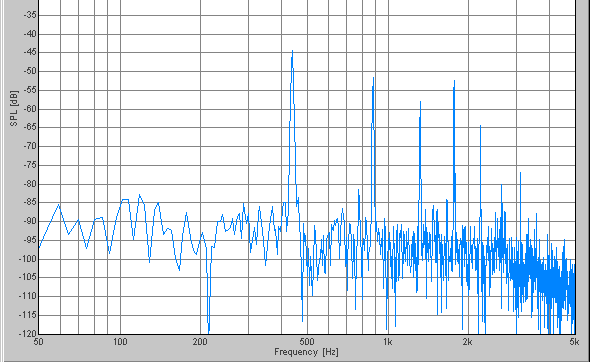
The peak frequencies of each scale are summarized on the table.
| A | 110 | 220 | 440 | 880 | 1760 | 3520 |
| B | 123.45 | 246.9 | 493.8 | 987.6 | 1975.2 | 3950.4 |
| C | 130.8 | 261.6 | 523.2 | 1046.4 | 2092.8 | 4185.6 |
| D | 146.825 | 293.65 | 587.3 | 1174.6 | 2349.2 | 4698.4 |
| E | 164.8 | 329.6 | 659.2 | 1318.4 | 2636.8 | 5273.6 |
| F | 174.6 | 349.2 | 698.4 | 1396.8 | 2793.6 | 5587.2 |
| G | 195.975 | 391.95 | 783.9 | 1567.8 | 3135.6 | 6271.2 |
Probably, the tuner judges the sound to be A, if 110, 220, 440, and 880 Hz are included. And if the sound contains 146.825, 293.65, 587.3, and 1174.6 Hz, it is judged to be D. I think that the comparison of the whole frequency pattern enables the distinction of scales, even if the two sounds contain the same frequency component.
November 2002