| Japanese | English |
その様子をRA(リアルタイムアナライザ)で再現してみましょう。

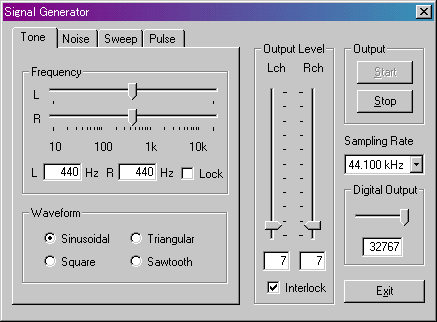
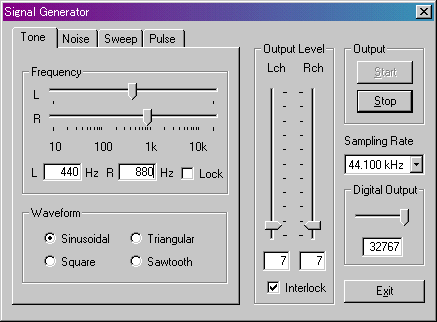
まず「シグナルジェネレータ」の「トーン」で左右のチャネルをA(440Hz)にセットし、それを「オシロスコープ」で見てみます。「オシロスコープ」ウィンドウ下部の「X-Y」をチェックします。
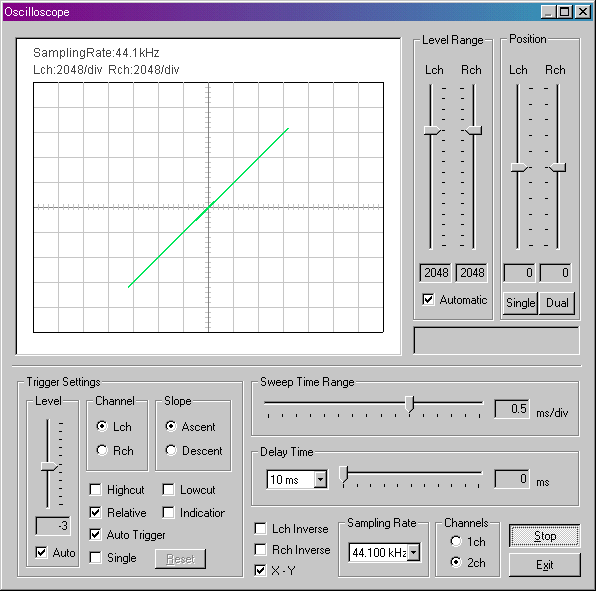
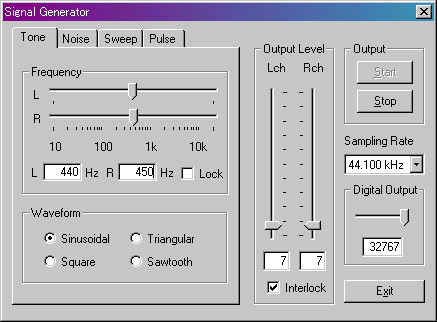
LRチャネルが同一周波数かつ同一波形であれば、このように静止して見えます。それでは片チャネルが450Hzだとどうなるでしょうか。
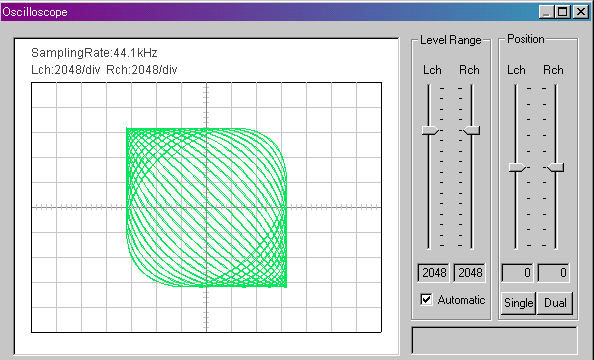
グラフの線は四角形の中をめまぐるしく動き回ります。それでも波形がおなじなので、オシロスコープに表われる形は幾何学的です。2chの周波数をX軸とY軸に割り当てたときに表示される図形を「リサージュ図形」といい、周波数を直感的にとらえるのに役立ちます。
Rチャネルの周波数をLチャネルの整数倍にするときれいです。倍音がきれいなハーモニーになることを目で納得することができます。数学が苦手な中高生に見せてあげてはいかがでしょうか。
周波数が一致しているかどうかでグラフがリアルタイムに変化するならば、ギターのチューニングに使えるかもしれません。
「楽器のチューニング-1」で使った方法で、Lチャネルに440Hzの正弦波、Rチャネルにギターの5弦を弾く音をマイクで入力します。
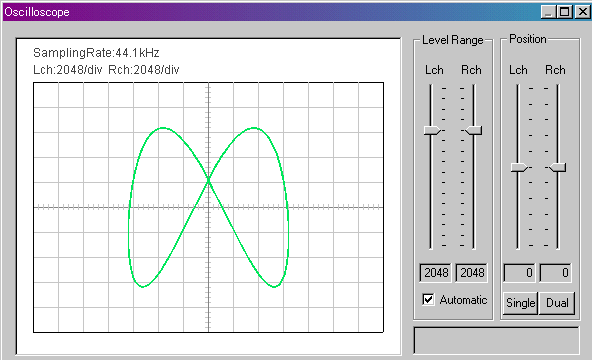
ギターの音が低いときのオシロスコープはこのように、めまぐるしく線が動き回ります。
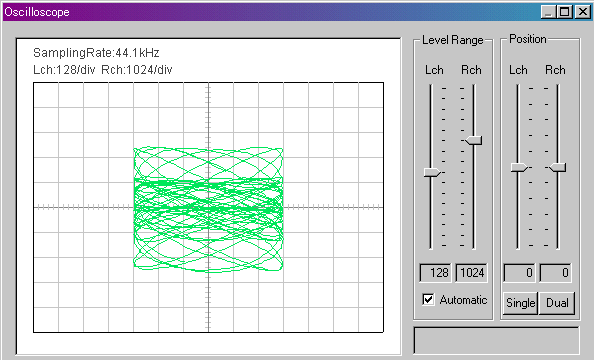
ギターの音が基準音に近づいてくると網のように細い線がすこしずつ束になって、動きが遅くなってきます。
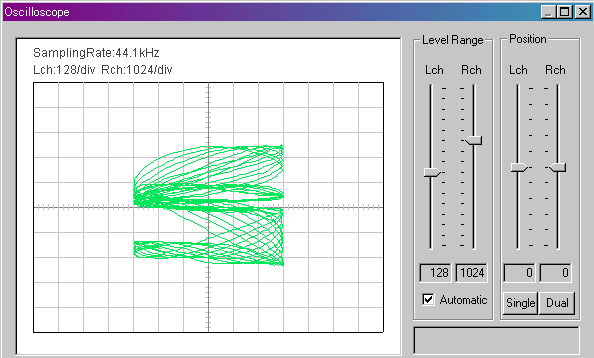
ギターの音が基準音に一致すると、太い線がメビウスの輪のようにつながってゆっくり回転します。静止しないのは、弦楽器の音は刻々と変化(減衰、共鳴など)しているからでしょうか。
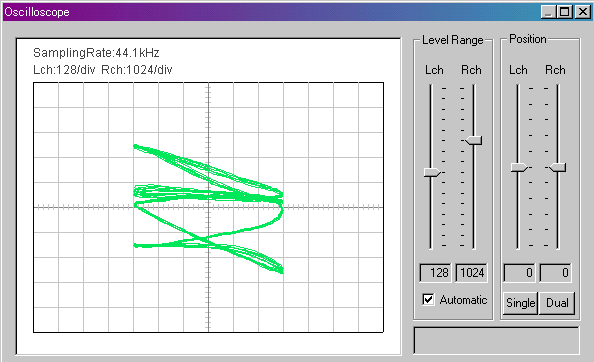
「オシロスコープ」の「X-Y」表示でチューニングしたときに表われる波形は楽器の音色を表わしているのでしょうか。前回のギターに対して、今回は電子ピアノを見てみます。Lチャネルに440Hzの正弦波、RチャネルにピアノのA(ラ)の音をマイクで入力してみました。
▼ A3
1オクターブ低いAです。輪が数回ねじれた状態で回っています。
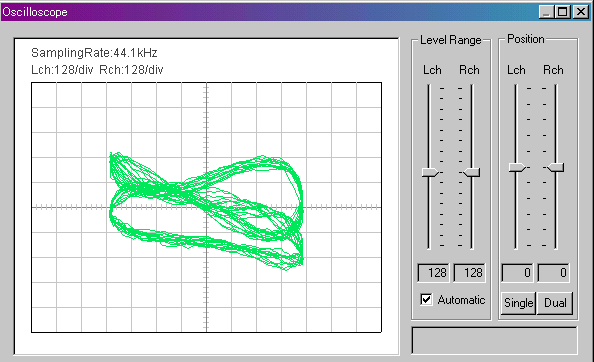
▼ A4
これがピアノの440Hzです。輪ゴムが回っているように見えます。
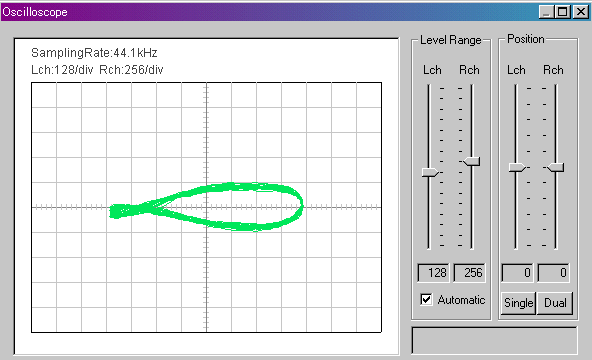
▼ A5
輪が1回だけねじれています。
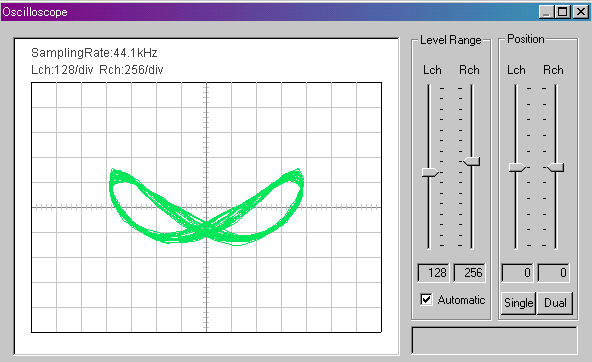
今度はRチャネルのピアノの音を、マイクではなく、ヘッドフォン端子から取ってみました。マイクよりはS/Nが良いのではないでしょうか。「オシロスコープ」の「X-Y」表示のチェックを外してみました。赤がピアノです。マイクで拾うよりは周期が目に見えます。
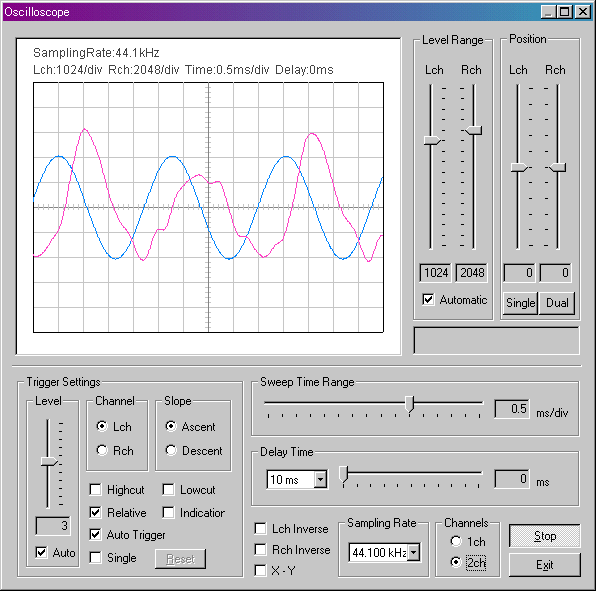
再度「X-Y」表示でピアノのAを見てみましょう。
▼ A3
マイク入力よりも線の束が太くなりました。ノイズが減ったということでしょうか。
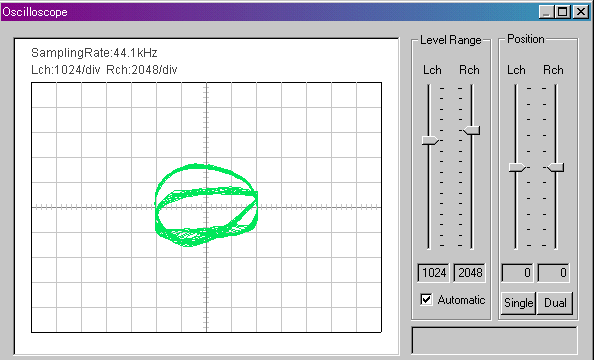
▼ A4
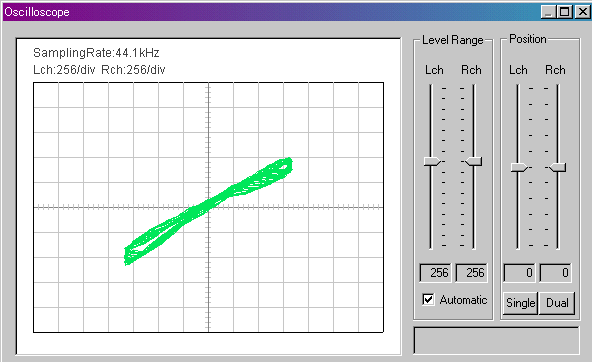
440Hzに同期する形に非常に近くなってきました。LRチャネルが完全に一致するとつぎのようなグラフになります。

「オシロスコープ」の「X-Y」表示に表われるグラフの形は楽器の種類によって異なるわけではなさそうです。ギターとピアノを比べても大きなちがいは見られません。
November 2002